吸收塔是利用溶解度的差异来分离气体混合物的操作。简单可以分为物理、化学吸收两种。
速率模型
在Aspen模拟中,有下列两种速率模型:
-
Kinetic:动力学反应模拟更贴合实际;塔内件持液量对非反应影响较大
-
Equilibrium:平衡反应,受限于精馏塔板上气液接触时间有限,很难达到反应平衡;实际反应受到传质速率影响,且过于理想化。
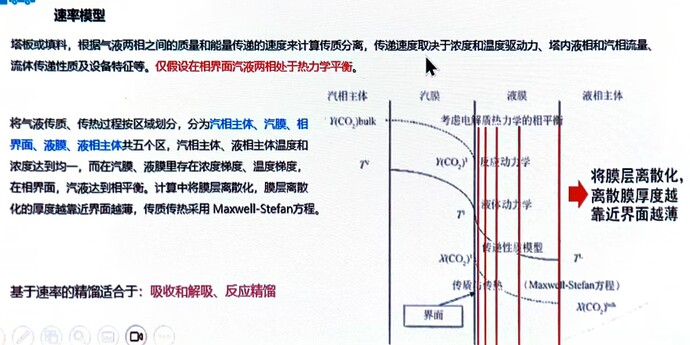
塔板或填料,根据气液两相之间的质量和能量传递的速度来计算传质分离,传递速度取决于浓度和温度驱动力、塔内液相和汽相流量、流体传递性质及设备特征等( 仅假设在相界面汽液两相处于热力学平衡 )。
将气液传质、传热过程按区域划分,分为 汽相主体、汽膜、相界面、液膜、液相主体 共五个区,汽相主体、液相主体温度和浓度达到均一,而在汽膜、液膜里存在浓度梯度、温度梯度在相界面,汽液达到相平衡。计算中将膜层离散化,膜层离散化的厚度越靠近界面越薄,传质传热采用 Maxwell-Stefan方程。
基于速率的精馏适合于:吸收和解吸、反应精馏。
双膜模型
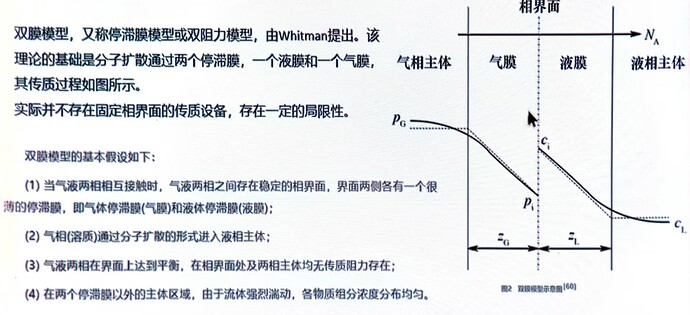
双膜模型,又称停滞膜模型或双阻力模型,由 Whitman 提出。该理论的基础是分子扩散通过两个停滞膜,一个液膜和一个气膜,其传质过程如图所示。
实际并不存在固定相界面的传质设备,存在一定的局限性。
双膜模型的基本假设如下:
- 当气波两相相互接触时,气波两相之间存在稳定的相界面,界面两侧各有一个很薄的停滞膜,即气体停滞膜(气膜)和液体停滞膜(液膜);
- 气相(溶质)通过分子扩散的形式进入液相主体;
- 气液两相在界面上达到平衡,在相界面处及两相主体均无传质阻力存在;
- 在两个停滞膜以外的主体区域,由于流体强烈湍动,各物质组分浓度分布均匀。
溶质渗透模型
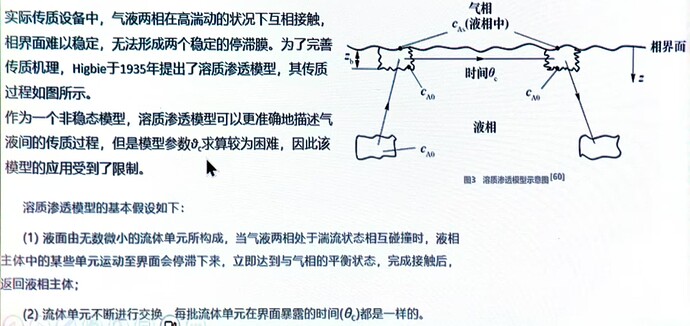
实际传质设备中,气液两相在高湍动的状况下互相接触,相界面难以稳定,无法形成两个稳定的停滞膜。为了完善传质机理,Higbie 于 1935 年提出了溶质渗透模型,其传质过程如图所示。
作为一个非稳态模型,溶质渗透模型可以更准确地描述气液间的传质过程,但是模型参数求算较为困难,因此该模型的应用受到了限制。
溶质渗透模型的基本假设如下:
-
液面由无数微小的流体单元所构成,当气液两相处于湍流状态相互碰撞时,液相主体中的某些单元运动至界面会停滞下来,立即达到与气相的平衡状态,完成接触后返回液相主体;
-
流体单元不断进行交换一每批流体单元在界面暴露的时间都是一样的。
渗透-表面更新模型
Danckwerts 于 1951 年在溶质渗透模型的基础上,提出了表面更新模型,又称为渗透-表面更新模型。
相较于溶质渗透模型,表面更新模型没有规定固定不变的停留时间,模型更贴近实际。此外,其模型参数表面更新率可以通过一定的方法测得,使得其离计算应用更进一步。
其基本假设如下:
-
该模型同样认为溶质向波相内部的传质为非稳态分子扩散过程,波面由无数微小的流体单元构成,但它否定表面上的流体单元有相同的暴露时间,而认为液体单元具有不同暴露时间,即存在年龄分布,界面上各种不同年龄的液面单元都存在,只是年龄越大者,占据的比例越小;
-
液面单元被置换的概率是均等的,即更新频率与年龄无关。
模拟计算膜阻力
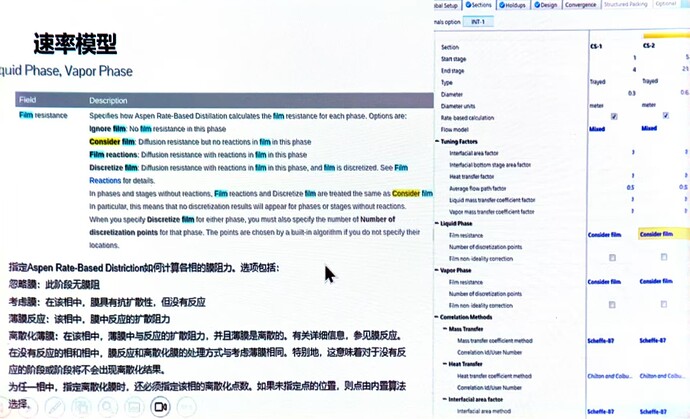
指定 Aspen Rate-Based Distriction 如何计算各相的膜阻力。
选项包括:
- 忽略膜:此阶段无膜阻
- 考虑膜:在该相中,膜具有抗扩散性,但没有反应
- 薄膜反应:该相中,膜中反应的扩散阻力
- 离散化薄膜:在该相中,薄膜中与反应的扩散阻力,并且薄膜是离散的。
有关详细信息,参见膜反应。在没有反应的相和相中,膜反应和离散化膜的处理方式与考虑薄膜相同。特别地,这意味着对于没有反应的阶段或阶段将不会出现离散化结果。
为任一相中,指定离散化膜时,还必须指定该相的离散化点数。如果未指定点的位置,则点由内置算法选择。