原创链接: EO,还是SM,是个问题——浅谈二者的区别点 。
已获得作者授权:
正文:
自我从事流程模拟工作时,就初步了解过建模时最常见也是最重要的两种求解方式:Equation Oriented(EO)联立方程法;和Sequential Modular(SM)序贯模块法。当然二者也可以联合使用,在AspenPlus中称之为Mixed Mode,通常叫做联立模块法。
在我之前多年的工作中,几乎没有碰到一位生产工程师询问过我关于EO的问题。但随着数字化转型的浪潮袭来,近些年被询问EO的次数多了起来。总结起来无非是两点:什么是EO?以及之前为什么不用EO或很少听见别人用EO?
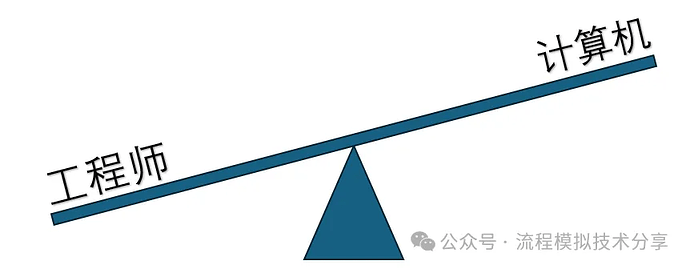
这种转变可以用一个跷跷板来描述:
当以离线应用为主时,“人”是应用的主体,那核心要求是怎么方便怎么简单怎么来,SM的求解方式便天然的被广泛使用。因为SM相较于EO的核心优点是:由于SM是按顺序计算流程中的每个模块,因此它天然的符合人们的逻辑思路,一步一步,一个一个的往下算,当出现错误或不收敛问题时,我们可以非常容易的定位到问题的所在,便于诊断分析。一句话,就是好学好用。反过来讲,这便是应用EO最大的挑战了,后面再讲它。
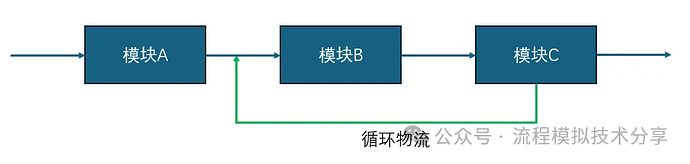
但有好就有坏。因为SM是顺序求解,所以当遇到循环物流时,便得反复迭代计算。
当遇到设计规定(或是Adjust,Controller)时也需要反复迭代计算。而“迭代”的出现便又引出了收敛容差设置(容差会累积)和数学算法选择的问题(例如加速、震荡与发散性)。如果循环物流较多,那又得选择出循环物流合适的位置,比如循环物流放在换热器的后面要比闪蒸罐的后面好的多得多,等等。进一步的,如果模型变得越来越复杂,例如存在多层内外嵌套循环,多个设计规定(或是Adjust,Controller),换热网络集成等;亦或者所求解的问题也越来越复杂,最典型的就是寻优和参数整定。那面对这种庞大问题求解所带来的最直接的挑战便是不易稳定的收敛和数小时的不断求解。此外,顺序求解所隐含的另一个问题便是参数的传递性,由前到后好算,由后到前难。
因此,如果应用的主体主要是工程师时,而求解的问题又没那么复杂时,SM的顺序求解所带来的方便性便可以碾压它的不足而被大家广泛的接受。
但时代在发展,形势比人强,事到如今我们越来越希望问题的处理都交给计算机,而把结果呈现给人们而进行判断和分析,以大幅提高生产效率——即数字化转型——模型的在线应用。此时天平来到了另一头:让计算机能更加快速地求解更复杂问题,而人不再是应用的主体。此时我们便对模型的求解速度有了更高的要求,例如实时优化(RTO)。所以EO的优势便有了更大的发挥场景:因为它将流程中所有模型的方程都放到了一起同时求解,因此它不存在“迭代”的问题。也因为这个优势,EO在模拟预测、参数整定以及寻优时,本质上都是一样的,所以它对越复杂的问题所展现出来的优势就越明显——都是在一个大型方程组中同时求解,只是变量的自由度设置不同而已,当然反向计算对它也不是问题。而SM本质上都是在反复计算,没有变量自由度的概念。
可即便是EO的求解优势如此巨大了,在线应用时依旧面临着它自始至终存在的挑战——难搞!这里的难搞主要是指哪怕在线模型采用EO求解,但它也不是一劳永逸的,还是需要工程师进行模型的离线维护。而一旦涉及到人,那人们对学习成本的要求又来了,此时此刻又会觉得还是SM好啊!
就拿最常见的工况研究为例。在 SM 模式下,工况研究就是通过逐步改变自变量的值(上下限及步长的规定下)重复执行流程求解来进行。而在EO模式中,工况研究问题就变成在当前稳态下的雅各比(JACOBIAN)矩阵,该矩阵包含每个变量的所有因变量的偏导数。可见二者求解模式的本质不同。问题越复杂,EO的优势便越大。
当模型发现不收敛时,对于SM而言顺着流程往下看,哪里不行点哪里;但是对于EO的不收敛问题,更多的需要依赖于自身数学的知识、经验和技巧。我们无法简单的从流程上入手分析,因为还是那句话:流程中的模型变成了一个大型方程组。所以EO的求解对初值敏感,如果初值偏离太大同样很难收敛。再比如EO所配变量之间的关系如果是不相关的,则会产生奇异性而不收敛。此外,EO不同于SM,如果参数配置不合理,循环设置不合理,闪蒸计算相关的变量设置不合理(例如温度、压力、气相分率、焓值),等等,就会在求解过程中出现奇点,由此也会造成各种收敛失败的问题,这都需要我们更多的从数学求解的过程和角度去分析问题的所在,而不是单纯的化工知识。如果在模型中加入自定义模块,那可能还需要进一步其分析其雅各比矩阵,稀疏性等,如果方程存在高度非线性,还得检查其是否具有连续性,否则一样很容易导致求解失败。如此等等。
所以我们不能简单的认为SM好,还是EO好;也不能说离线使用就用SM,在线应用(例如实时优化)就用EO,归根结底还是要看具体情况而言。
如果你的问题不复杂,比如仅有少量的循环,那实际上使用SM要更加方便的多,在当前计算机性能的加持下,即便是不断的迭代计算也花不了多少时间,更重要的是模型的可维护性也高(容易掌握和排查问题)。但是如果你的模型很复杂,比如像合成氨、EO/EG、带换热网络的常减压等装置,需要进行多变量寻优,同时对模型的求解时间又有要求,那EO便是不错的选择。但它的可维护性上需要做一权衡。无法维护的模型等于没模型。
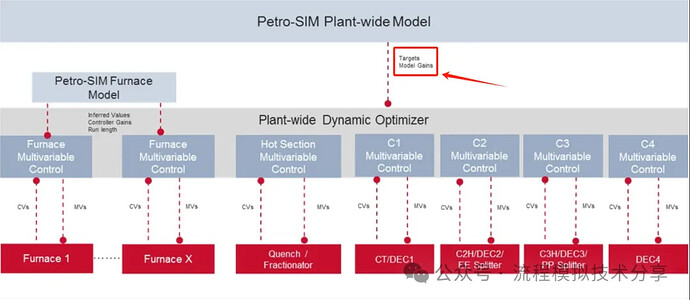
话说回来,我们当然希望既要也要。所以在面对SM对于复杂问题时存在求解时间过长,寻优很容易陷入局部最优等挑战时,我个人的解决策略是通过重构模型后使用全局优化算法(例如遗传算法、粒子群优化等)计算出“最优初值”后代入SM模型中仅在少幅扰动下计算求得最优值。顺便提一句,横河/KBC的RTO技术采用的是通过Petro-SIM“内推计算”和“增益更新”的概念来解决这一问题,当然更具体的技术细节我也很好奇,之前尝试编代码复现技术路径但失败了,尚未参透到底是咋算的。
图自横河官网《Dynamic Real Time Optimizer (RT-OP)》一文
而对于EO而言,目前所听到的对其有更深入推进的是中控技术股份有限公司的中控流程工业过程模拟与设计平台(APEX)。其官方宣传是:中控APEX采用联立方程建模方法,区别于传统的序贯模块法,通过特有的初值策略、流股连接策略、自由度分析以及目标函数组态等功能,可一次性得到全局协调的收敛方案,大幅优化计算效率,更加适应于多应用场景的复杂流程的模拟与优化。希望后面有机会能做一对比计算。
所以期待不远的将来,又快又方便的算法能够在流程模拟软件中普及开来,让我们不再痛苦于数学问题而专注于工艺问题本身!不过话又又说回来,无论什么算法,机理模型本身的准确性可是基石,它不准了啥算法都白搭。